The sun emits light from the photosphere, physically, photons can be emitted anywhere from the bottom of this layer right to the border. If the photon is recaptured in the photosphere it heats the material and the material can then reemit the photon if the material is hot enough.

Essentially, the sun is a light source with a material covering it, this material has subsurface scattering.

Naively, one could assume that the surface of the photosphere emits light perpendicularly outwards. And that the intensity drops as the surface "turns away" from the observer. The intensity of light can thus be modelled as such: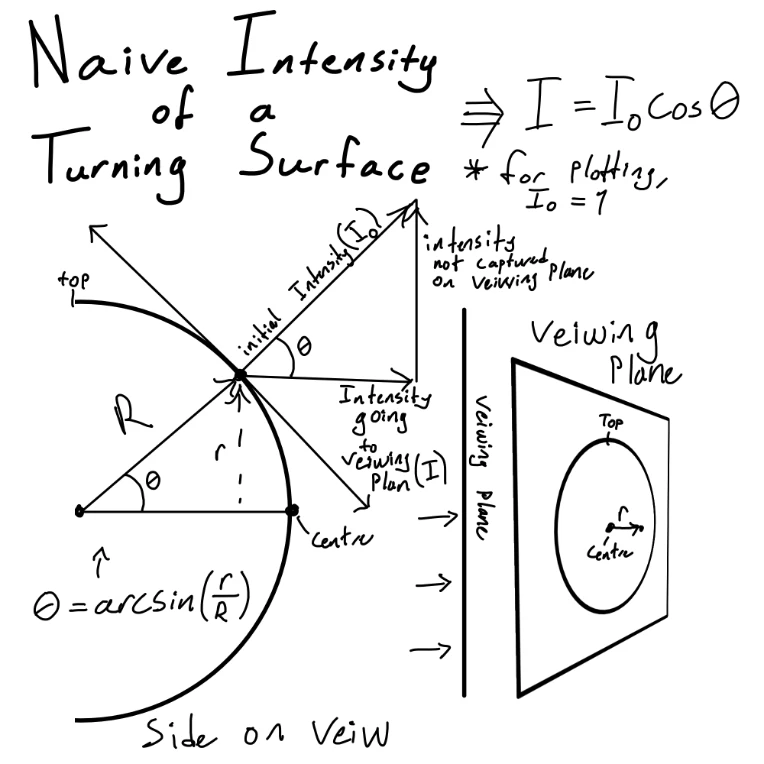

To demonstrate the unaccounted "subsurface scattering" of the photosphere, consider the overly general case of some amount of light at frequency 'f' (developing the accurate model with frequencies of light in mind means that false color images can be simulated well later on) in one dimensions:

For a better surface simulation a 3d model needs to be developed that takes into account the viewing angle.

oh and don't worry about the unknown coefficients, they have been found already by the people that came up with this stuff.

So ignoring all that for now, using python, I wrote up some code that (using matplotlib as the renderer) can simulate the surface of the sun. Basically calculating measured intensity on every point of the viewing plane, and then plotting it...

Smaller simulation, looks chunky so increase the simulation size:

The top one is the surface I simulated, and the bottom one is a real picture (I found on the internet).

firstly ignore real phenomena, the real picture looks staticy because the real sun's photosphere is convective, so it boils, creating granules, the black spots are sun spots, and unless I simulate the magnetic field lines and the convection it'll be beyond my surface simulations.

To the untrained eye they look very similar, however the edges on the real image are brighter, this is because of the subsurface scattering, so the simulated image looks like a solid ball lit from the observer's direction

Now that I have a brute force renderer, I might create a much more real simulation.